Blog

In this post, I want to briefly introduce Differential Privacy to you, which, in my honest opinion, needs to get more attention in the software developer community.

During my Master thesis, I evaluated the use of Differential Privacy for Federated Learning (I might explain Federated Learning in another post).

The Theory

Differential Privacy, originally $\epsilon$-Differential Privacy (DP)¹, is a way to secure the privacy of individuals in a statistical database. A statistical database is a database, where only aggregation functions like “sum”, “average”, “count”, et cetera… can be executed. DP basically perturbs a statistical output of such a function applied to a database to provide anonymity. The result of the function should still be statistically useful but noisy such that the output can not be linked to a certain individual in the database anymore. Mathematically speaking, DP ensures that:

$$\forall t \in Range(F): \frac{Pr[F(D)=t]}{Pr[F(D’)=t]} \leq e^\epsilon$$

Given:

1. Two neighboring databases $D$ and $D’$ which only differ at one individual. That means $D’$ can be obtained by removing one entry from $D$.
2. A statistical Function which queries the database in an aggregating manner. For example, $F$ could be the average of a certain attribute over every entry from $D$.

The equation² says: The probability to receive any result $t$ on applying $F$ on $D$ should be relatively equal (bound by $\epsilon$) to the probability to receive the same $t$ on applying $F$ on $D’$.

In other words: the smaller $\epsilon$ is, the better the privacy. If $\epsilon=0$ the function $F$ would not depend on its parameter $D$ anymore and is thus useless. So $\epsilon$ should be small but not zero.

The smaller $\epsilon$ the fewer impact has a single individual on the output of function $F$.

To you statistics fans: This equation is basically a bounded statistical divergence.

Why do we need that?

In times of Machine Learning and Big Data, we are in a situation where many companies are hoarding lots of data (not only from their direct customers). We want to gain knowledge out of these datasets but don’t want to violate each individual’s privacy in the data. Furthermore, different governmental restrictions like the GDPR instructs companies to let their customers opt-out. It is, however, hardly feasible to opt-out individuals from an already trained ML model. Instead of opting-out, DP suggests keeping the impact of individuals on a statistical function to a minimum.

Differentially Private Mechanisms

I am going to introduce two simple examples to apply DP on statistical databases and then briefly outline how we can transfer these techniques to machine learning.

AIDS survey

This one is the school book example when first researching DP. Consider you want to find out how large the fraction of people having AIDS in a certain population is. Considering this a pretty sensitive information, the participant is likely to deny an answer (Response Bias). Your actual workflow is: approaching the respondent to write down yes or no, whether he has AIDS or not.

But let’s consider you don’t ask them to answer with yes or no but you rather let them toss a coin. When the coin shows heads on the first throw, then the patient writes down the truth. If the coin toss is tails he tosses the coin again and answers yes or no whether the coin shows heads or tails on the second throw³.

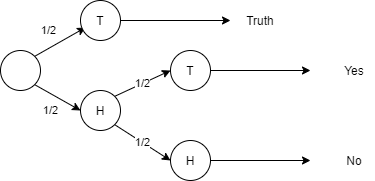
In the above picture, I wrote down the probability tree. This technique is called Randomized Response and is a popular $\epsilon$-DP mechanism.

1. How do we get a meaningful answer from our noisy data?

   As you noticed, the data we will get is perturbed in a systematical way, in other words, we traded privacy with statistical utility. We can’t find the true fraction $p$ of people having AIDS but we can come up with an approximative estimator $\hat{p}$ which can be calculated as follows:

   $$Pr[Response=Yes] = \frac{1}{4} + \frac{1}{2} \cdot \hat{p} \Rightarrow \hat{p} = (Pr[Response=Yes]-\frac{1}{4}) \cdot 2$$

2. But what $\epsilon$ does that give us?

   We can simply insert the probabilities of our true results and the fraction of perturbed results in the original DP equation from above:

   $$\frac{Pr[Response=Yes|Truth=Yes]}{Pr[Response=Yes|Truth=No]} = \frac{1/2+1/4}{1/4} = 3$$

   That means we have a $\epsilon = \ln(3)$-differentially private mechanism.

We see here, that the essential principle of DP is Plausible Deniability. Every individual can plausibly deny its sensitive information. In this case, an individual who answered yes (for having AIDS), when questioned, could refer to a second coin toss.

Hospital data

So far we have found out, how we can retain privacy with a dataset $D$, which consists only of boolean values, but what about real numbered values? Imagine a hospital having a large dataset $D$ with lung cancer patients. We want to apply a function $F$ to give us the average of cigarettes each patient smoked per day e.g. a governmental survey. We don’t want the government to get sensitive information about the dataset. But imagine if the government queries $F$ on a certain day and then on another for a second time and in between these two queries, a patient $x$ left the hospital (and opted out of $D$ yielding $D’$) they can easily infer how many cigarettes patient $x$ smoked. Admittedly, this example is a little far fetched, but I hope it suits you to visualize the problem.

How can we preserve privacy in this case?

First, let’s imagine the probability of $F$. Since currently $F$ only depends on a dataset, the probability of $F(D)$ is $1$ for a single output $t$. The probability of $F(D’)$ is $1$ for a potentially different $t’$. The probability distribution of $F$ is a point mass distribution. The entire probability mass lies in a single output.

But remember: In DP, we want for every possible $t$ the probability for $F(D)=t$ and $F(D’)=t$ to be very similar. The solution is, we need to apply noise from a continuous distribution to the function $F$ s.t. every possible outcome $t$ could be from either $F(D)$ or $F(D’)$ (Plausible Deniability).

In this example we will use the Laplace Mechanism:

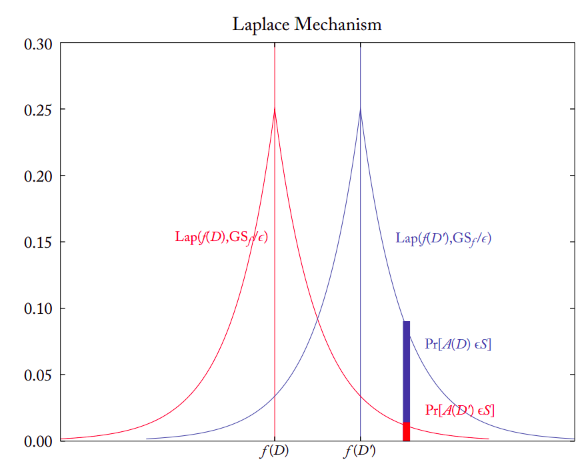
As we see in the plot above², we can easily add noise sampled from a Laplace distribution to the result on $F$. Although, because we can’t confirm the DP-bound for every possible neighboring database $D’$, we need to find the Global Sensitivity ($GS$), that is, the maximum difference we get when we remove a certain $x \in D$ w.r.t. $F$. Imagine a function to count each individual in a database. The maximum change you could get by removing an individual is exactly $1$.

Each result we get from the two distributions, could either be from $F(D)$ or $F(D’)$, which basically is again Plausible Deniability

Differentially Private Machine Learning

It turns out, that we can easily apply $\epsilon$-DP to Machine Learning. Overall there are two ways:

1. Local Differential Privacy

   Here we perturb every single entry in our training dataset before we feed it into the training of our model. We can do this, by just applying the above discussed mechanisms. This method is preferred if you e.g. don’t trust your cloud ML provider like Azure ML.

   In my experiments, I used the Labelled Faces in the Wild dataset⁴ and perturbed each pixel⁵ using the Laplace Mechanism.

2. Central Differential Privacy

   In CDP, we apply noise to our training function. For example, during the optimization step, we could add noise sampled from a scalar probabilistic distribution to our gradients. State-of-the-art research suggests using a Gaussian mechanism where noise is sampled from a Gaussian distribution and added to the gradients.

   But because we can’t determine the global sensitivity of the gradients beforehand, we need to clip the gradients to a maximum value. Tensorflow Privacy is a pretty good extension to Tensorflow that just does that. I recommend reading this small Tutorial One problem arises due to the use of CDP which is not trivial: We only talked about the anonymity of $F$ for a single query, but imagine an attacker who queries $F$ multiple times, he is eventually able to average the real value. Consider the Laplace distribution, with more and more queries, if we average the results, we eventually end up with the true mean. In CDP depending on how often the optimizer steps over a certain individual, the lower the privacy guarantee will end up. For that case, we need a privacy accountant.

Taken from Bernau et al.⁵ we can see in the following plot the decrease in accuracy with increasing privacy guarantee of a classifier trained on the Texas Hospital Stays dataset⁶.

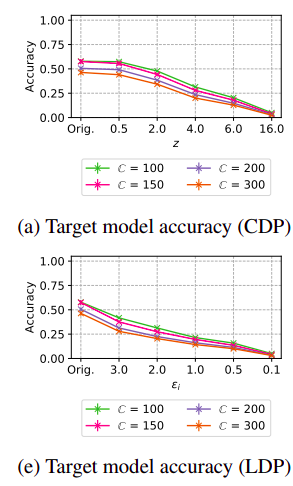
Mind that Bernau et al.⁵ didn’t specify the CDP $\epsilon$ values in the plot, but the noise multiplier for the Gaussian Mechanism. The corresponding $\epsilon$ values are approximately $250, 6.5, 2, 1, 0.3$. $\mathcal{C}$ denotes different number of output labels for a classifier. The larger the noise multiplier, the more complex the model. The more complex the model is, the faster it tends to have a decrease in accuracy with DP applied.

Depending on the $\epsilon$ value, the utility of our final ML model (i.e. the accuracy) worsens. To assess a good trade-off between privacy and utility, in my thesis I am using different threat models like:

• Membership Inference Attacks by Nasr et al.⁷ as evaluated from Bernau et al. ⁵
• Attribute Inference Attacks by Yeom et al. ⁸

It turns out, that these attacks do not only get worse depending on $\epsilon$ but can also be used pretty easy to evaluate the effective privacy of an ML model. But these attacks are subject to another blog post.