Blog
Did you ever wonder what it would look like if we combine a chair and an airplane? Turns out it doesn’t look that good.
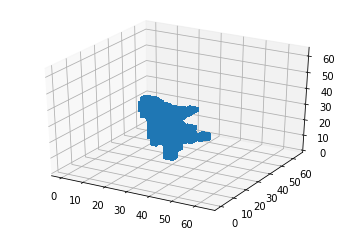
Before we get to this Chairplane, lets first outline this post’s topic: I am going to demonstrate you some possibilities of an 3D Generative Adversarial Network. That is: A GAN not applied to images, but to 3D Voxel objects.
But what is a GAN?
A GAN consists of two deep neural networks that try to game each other.
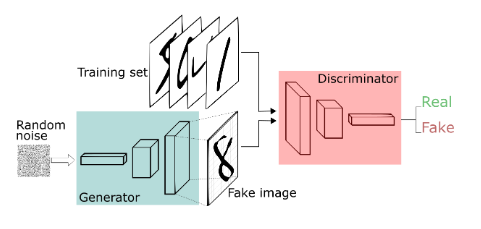
At it’s heart, we have a Generator and a Discriminator. Given a dataset of e.g. images, we train the Generator to create new samples that just look like the original images. And we train the discriminator to distinguish between the original and the ones from the Generator a.k.a. fake images. In practice, these two models are actually one model, more concretely: Two neural nets stacked together. The training follows these simple steps:
- sample a random vector z
- feed z into the generator yielding some kind of image
- sample an original image and feed it into the discriminator
- Discriminator should output 1 for original, using e.g. Cross-Entropy
- train the Generator and the Discriminator using the error from the Discriminator
- take a fake image from the Generator and feed it into the Discriminator
- Discriminator should output 0 for fake, using same Loss function to train Generator and Discriminator
- Repeat
That’s it basically. Athough, the interesting part is, that the Generator gets better and better generating similar images and the Discriminator gets better and better distinguishing original and fake images. However, in practice it’s hard to reach a convergence, in my experiments sometimes the Discriminator is just way better than the Generator, and the Generator was not able to extract enough information during the training from the Discriminators gradients. If it eventually reaches an equilibrium, the Generator has a cool property: It learned a very compact representation of the learned images. That is the vector z or also called latent space. This vector encodes all information for the Generator needed, to generate a certain image. The topic itself is a bit more complex, and this is just a brief introduction, however it covers the most important aspects imho. Lastly, there is a strong thematical connection to something called Autoencoders, which I maybe get to in another post.
But what is a 3D-GAN
An image usually consists of three-dimensional tensor, the x-direction, y-direction and the channels. That is at least the case for colourful images, in a greyscale image the tensor would be plain two-dimensional. This is due to the fact, that e.g. in the RGB-system we have three colour channels. Which result in an additive colour system. In a greyscale system however, each pixel can only take a value between 0-255 or 0-1.
But for the sake of simplicity, lets consider we have a greyscale 3D Volumetric object. We would have a third dimension for the z-direction.
Interpolation
The reason for my experiments, was to examine how it would be possible to interpolate different 3D-Voxel objects in the latent space. My idea is to have some kind of vector arithemtic using the z-vectors of known 3D Objects:
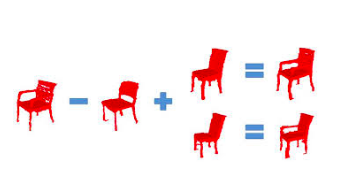
Turns out that this works, depending on the quality of your GAN model of course.
Implementation
In my experiments I’ve used comms4995-project. The Generator consists of four 3D-Deconvolutional Layers and the Discriminator consisting of four 3D-Convolutional layers. I simplified the code and put everything including my results into a single notebook. For running the model without training you can clone my repo and run the install.sh. The 3D data is taken from csail btw.
Results
My first experiment was interpolating between two 3D chairs:
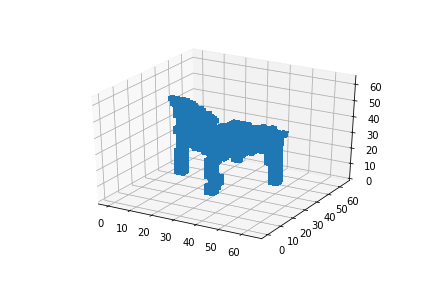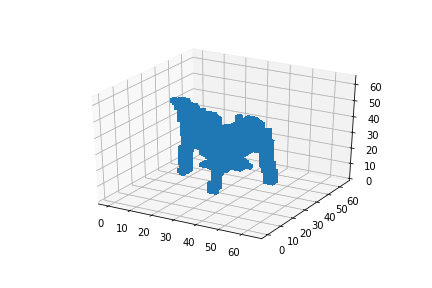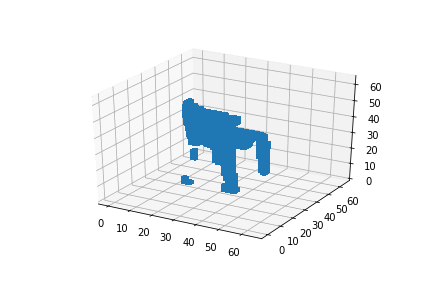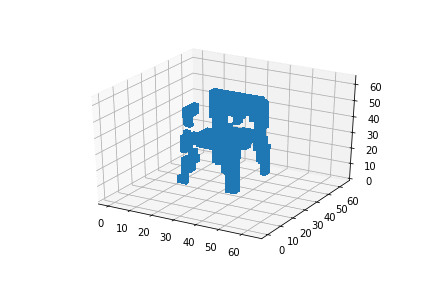
My second experiment, interpolating between an airplane and a chair didn’t work as good as expected, as you could see in this post’s introduction. But why is that so?
During training, the z vector gets sampled randomly, but it turns out, that the z-vectors from the chairs build a seperate cluster compared to the z vectors corresponding to an airplane, in the latentspace. Intuitively, that is because a vector z that already generated a good chair and a newly seen vector z’ that is very close to z is more likely to generate a chair as well. It would take a big step from the optimizer to change the weights, s.t. z’ generates an airplane and z still generates a chair.
It is possible to visualize these clusters using e.g. t-SNE or other embeddings. Like this guy shows in his medium post. Although, in my 3D-case, I sadly couldn’t reproduce such visualisation as seen in the next image:
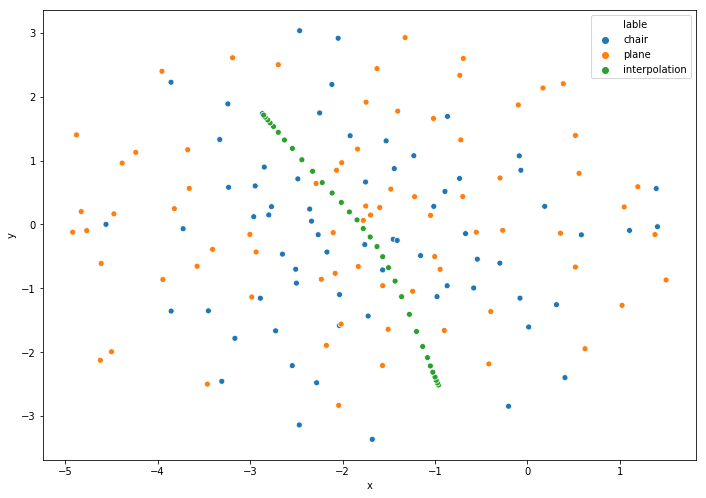
Conclusion
Interpolation with GANs is a pretty cool thing and works already in many areas, for example:
However, generating and interpolating between 3D voxel objects, e.g. for human pose generation, seems to need a bit more research.
Further read: